Understanding viscoelasticity in just a few minutes…
Polymeric materials possess significant vibration-energy dissipation capabilities. They are used to protect structures, equipment and passengers from vibrations, shock and noise.
Challenges Related to the Experimental Characterisation of Viscoelastic Materials
In order to characterise these materials their dynamic stiffness and loss angle are typically represented according to the loading frequency. These experimental observations highlight a noticeable evolution of these values depending on the frequency ranges (figure 2).
Figure 2: frequency representations
The experimental characterisation of these properties — dynamic mechanical analysis — is a delicate process because the frequency range that testing should cover is often very broad and difficult to access with a single experimental device. Besides, the mechanical properties of viscoelastic materials are highly temperature-dependent. One solution consists in using the time-temperature superposition principle. This method is based on vibration tests covering a relatively narrow frequency range and conducted at various temperatures. Time-temperature superposition then enables to reconstruct the dynamic behaviour of a given material over a broad frequency range and at a given temperature.
There are several measurement biases with this method. The main one stems from the time-temperature superposition hypothesis which is not applicable to all materials. Time-temperature superposition is not relevant anymore for modern materials that have emerged from the industrial world such as multilayer materials, filled polymers, functionalised materials or structural adhesives. Therefore, the temperatures and frequency ranges used for testing must be consistent with the real-life operating conditions of such materials in order to characterise their dynamic properties.
For several decades the VAST team has been developing innovative, high-performance viscoanalysers that enable to characterise the dynamic mechanical properties of these materials directly and under different loading configurations (tension-compression, shear, combined static and dynamic loading, etc.) These new experimental technologies (figure 3) currently allow for the direct characterisation of viscoelastic materials up to 10 kHz (without using time-temperature superposition or modes that are specific to the experimental device).
Figure 3: three viscoanalysers developed at Supméca
Therefore, conducting these tests at various preload values and loading amplitudes enables to characterise the nonlinear viscoelasticity of the studied material precisely.
The quality of the experimental data acquired from these tests is a key issue when predicting the dynamic behaviours of the components and structures that these viscoelastic materials are used in.
Challenges Related to the Modelling of Viscoelastic Materials
The main purpose of acquiring experimental data on the dynamic behaviours of viscoelastic materials is to feed prediction models for components, structures or systems.
Viscoelastic mechanical behaviours can be separated in two main categories of models: those based on fractional derivatives and those based on elementary rheological components such as the Generalized Maxwell model.
The first bottleneck, modelling-bottleneck, stems from the identification of the parameters of these models. This point is covered in several publications of the VAST team [1 – 3] and valued by several industrial partners (Hutchinson, BOSCH braking systems, AER, ADERIS).
The second bottleneck tackled by the VAST team concerns the integration of these models into commercial, structure calculation codes [4, 5].
Viscoelasticity has been a particularly active research-area for decades. New fields of study are currently emerging with functionalised materials, metamaterials, additive manufacturing and bio-based or environment-friendly and sustainable-development compatible materials.
[1] J.-L. Dion and S. Vialard, “Identification or rubber shock absorber mounts,” Mécanique industrielle et matériaux, vol. 50, no. 5, pp. 232–237, 1997.
[2] F. Renaud, J.-L. Dion, G. Chevallier, I. Tawfiq, and R. Lemaire, “A new identification method of viscoelastic behavior: Application to the generalized maxwell model,” Mechanical Systems and Signal Processing, vol. 25, no. 3, pp. 991 – 1010, 2011.
[3] H. Jrad, J. L. Dion, F. Renaud, I. Tawfiq, and M. Haddar, “Experimental characterization, modeling and parametric identification of the non linear dynamic behavior of viscoelastic components,” European Journal of Mechanics – A/Solids, vol. 42, no. 0, pp. 176 – 187, 2013.
[4] S. Thouviot, G. Chevallier, F. Renaud, J.-L. Dion, and R. Lemaire, “Prise en compte des comportements viscoélastiques dans la simulation dynamique des systèmes de freinage,” Mechanics & Industry, vol. 10, no. 05, pp. 385–396, 2009.
[5] H. Festjens, G. Chevallier, F. Renaud, J.-L. Dion, and R. Lemaire, “Effectiveness of multilayer viscoelastic insulators to prevent occurrences of brake squeal: A numerical study,” Applied Acoustics, vol. 73, no. 11, pp. 1121 – 1128, 2012.
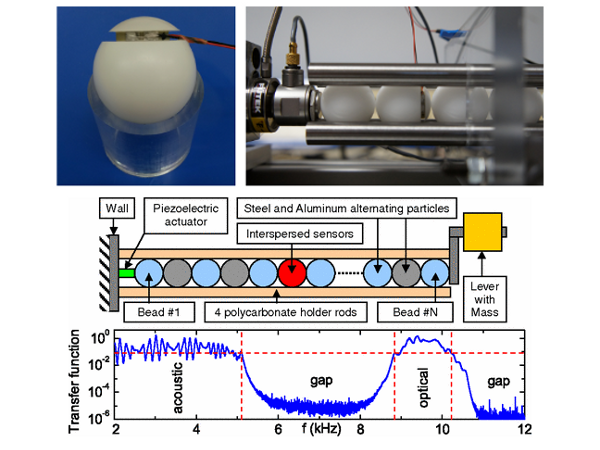
Vibration analysis is of prime importance for mechanical systems and structures in order to determine their behaviour in operating conditions or subsequently to exceptional events. Therefore, conducting experimental studies on the vibrations occurring in a system (be it mechanical, aeronautical or civil) is now an essential step of the design and monitoring processes. To this end, in addition to standard measurement tools such as piezoelectric accelerometers, laser motion sensors and laser vibrometers, high-speed camera systems appear to be promising because of the contactless recording of large scenes at very high rates, even thousands of frames per second.
